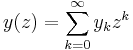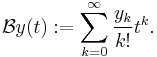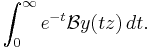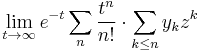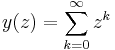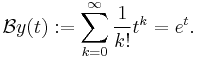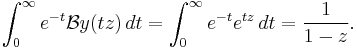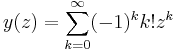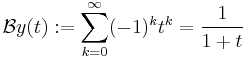Borel summation

Borel, then an unknown young man, discovered that his summation method gave the 'right' answer for many classical divergent series. He decided to make a pilgrimage to Stockholm to see Mittag-Leffler, who was the recognized lord of complex analysis. Mittag-Leffler listened politely to what Borel had to say and then, placing his hand upon the complete works by Weierstrass, his teacher, he said in Latin, 'The Master forbids it'.

Mark Kac, quoted by Reed & Simon (1978, p. 38)

In mathematics, Borel summation is a summation method for divergent series, introduced by Emile Borel (1899). There are several variations of this method that are also called Borel summation.

Contents

Definition

Let

y(z) = \sum_{k = 0}^\infty y_kz^k

be a formal power series in z.

Define the Borel transform \mathcal{B}y of y by

\mathcal{B}y(t)�:= \sum_{k=0}^\infty \frac{y_k}{k!}t^k.

Suppose that the Borel transform converges to an analytic function near 0 that can be analytically continued along the positive real axis to a function growing sufficiently slowly that the following integral is well defined (as an improper integral). Then the Borel sum of y is given by

\int_0^\infty e^{-t} \mathcal{B}y(tz) \, dt.

A slightly weaker form of Borel's summation method gives the Borel sum of y as

\lim_{t\rightarrow\infty} e^{-t}\sum_n\frac{t^n}{n!}\cdot\sum_{k\le n}y_kz^k

If the sum exists in this sense then it also exists in the previous sense and is the same, but there are some series that can be summed with the previous method but not with this method (Hardy 1992, 8.5).

Examples

The series

y(z) = \sum_{k = 0}^\infty z^k

converges to 1/(1-z) for |z|<1. The Borel transform is

\mathcal{B}y(t)�:= \sum_{k=0}^\infty \frac{1}{k!}t^k = e^t.

So the Borel sum is

\int_0^\infty e^{-t}\mathcal{B}y(tz) \, dt = \int_0^\infty e^{-t} e^{tz} \, dt =\frac{1}{1-z}.

which converges to 1/(1-z) in the larger region Re(z)<1, giving an analytic continuation of the original series.

The series

y(z) = \sum_{k = 0}^\infty (-1)^kk!z^k

does not converge for any nonzero z. The Borel transform is

\mathcal{B}y(t)�:= \sum_{k=0}^\infty (-1)^kt^k = \frac{1}{1%2Bt}

for |t|<1, and this can be analytically continued to all t≥0. So the Borel sum is

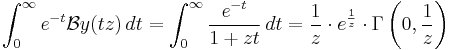\int_0^\infty e^{-t}\mathcal{B}y(tz) \, dt = \int_0^\infty \frac{e^{-t}} {1%2Bzt} \, dt = \frac 1 z \cdot e^\frac 1 z \cdot \Gamma\left(0,\frac 1 z \right) (where Γ is the incomplete Gamma function).

This integral converges for all z≥0, so the original divergent series is Borel summable for all such z. This function has an asymptotic expansion as z tends to 0 that is given by the original divergent series. This is a typical example of the fact that Borel summation will sometimes "correctly" sum divergent asymptotic expansions.

The Borel polygon

The region where the power series of an analytic function is Borel summable was described as follows by Borel and Phragmen (Sansone & Gerretsen 1960, 8.3).

If y is a power series that converges in some neighborhood of the origin then it has a Borel sum at some point z if it can be analytically continued to a disc with diameter 0z. Conversely if the function can be analytically continued to the disc with diameter 0z then it is Borel summable at z.

The set of points z such that the function can be analytically continued to the interior of the disk with diameter 0z is a polygon when the function has only a finite number of singularities, called the Borel polygon. Its edges pass through the singular points and are orthogonal to lines joining the singular points to 0.

Applications

Borel summation finds application in perturbation expansions in quantum field theory. In particular in 2-dimensional Euclidean field theory the Schwinger functions can often be recovered from their perturbation series using Borel summation (Glimm & Jaffe 1987, p. 461). Some of the singularities of the Borel transform are related to instantons and renormalons in quantum field theory (Weinberg 2005, 20.7).

Notes

See also

References